공부 정리 블로그
[Chapter9]언어모델(2) - back-off, perplexity 본문
언어모델 review


이 방법의 문제점은?
1. 메모리
2. 학습 데이터 부족
3. 분자 분모 0 -> 언어 모델의 확률 값이 0이 되어버리므로, 음향 모델을 잘 만들어도 단어 tuple에 대한 count 가 0이 되어버림
Discounting & backoff로 해결
언어모델이 0이 되는 것을 방지
unseen 에 해당하는 결과지만, <s> buy sell </s>
P(W) = P(buy|<s>) * P(sell|buy) *P(</s>|sell)
EM에 의해서 계산해보면 0 이 돼버리므로, 음향모델을 아무리 잘 만들어도 언어모델 확률이 0 -> 문장 확률 0
문제는 39개의 unseen을 어떻게 줄 것인가?
ㅇ Laplace smoothing
- 전부 counting 1씩 증가
- 성능은 안 좋음



원래 확률 1(EM 일때) -> 7/13 으로 줄어듦
Seen 확률 감소 / unseen 확률 증가
문제점
- 1씩 더한 근거가 없음(성능 떨어짐)
- 이해하긴 쉬움
Add-k smoothing
- 1을 더하는 대신 1보다 작은 수 k를 더함
- Add 1 보다는 성능 좋지만 성능 떨어짐(적절한 k에 대한 근거가 없음)
Good turing smoothing
- r번 만큼 나오던 것의 count를 바꿔줌
ex) C(buy the) = 6 을
- unique한 단어들 셈 unigram
총 단어에서 전체 corpus size N=615876 일 때,
unique(Unigram) 한 것의 개수를 구해서 누적해서 count를 셈 V = 14585
관측된 seen bigram tuple의 개수 : Seen bigram = 138741(1번) + 25413(2번) + 10531(3번) + 5997(4번) + .. = 199252
전체 중 199252개의 seen bigram tuple은 관측이 되었고
smoothing을 해줄 unseen(r=0)인 것들의 개수를 구함
n_0(unseen tuple) = 14585^2 - 199252 = 212522973
unseen tuple count 재조정(0이 나오는 것을 방지하기 위해) : C_GT(Unseen) = (0+1) *(n_1/n_2) = 0.00065
unseen 에 대한 bigram 확률 : C_GT(Unseen) / N


ㅇ 문제점
- 모든 카운트들을 대체할 수 없다 (n_(r+1) = 0인 경우 nr 추정 x)
r -> (r+1) *((n_(r+1)/n_r) 로 대체
가정: 학습 자료가 엄청 큼
(??)
count >1 인 것에 대해 작게 만드려는 상황
corpus가 유한하기 때문에 unseen한테 주려하고 있고,
이상적인 dr은 0~1사이가 돼어야 기존 값보다 작은 값으로 만들어 줄 수 있는데, 실제는 학습 자료가 유한하므로, 예외처리가 들어가야함 (SRI LM)
9.1.2 Back-Off 언어모델
학습 데이터에서 tri-gram tuple 안나타났을 때 ? => 이 튜플은 안 나타는 거라고 얘기할 수도 없는 거임

어떤 language 모델 확률값(ex. tri-gram)이 안정적으로 구해지지 않을 때,
이용하려고 했던 모델보다 표현력은 안 좋지만 안정적으로 추정가능한 모델(bigram x penalty)을 써서 확률을 계산하는 방법
trigram이 표현력이 더 좋음(bigram으로 trigram을 만들 수 없음. 반대는 가능)
하지만 bigram이 표현력이 떨어지지만 안정적으로 추정 가능. 가능한 개수를 각각 살펴보면 bigram의 경우가 훨씬 적으므로
같은 양의 corpus에서도 추정해야하는 개수가 작아 안정적으로 추정 가능
unigram도 안 나오는 경우(안정적으로 추론이 안되는 경우는 없음), 수동으로 채워줄 수 있음. 손으로 집어 넣을 수 있기 때문에 안정적임
Katz back-off
A, B 집합으로 나누어서 한다
ㅇ 출현 횟수가 K 이하의 n-gram의 출현 횟수의 합을 m이라 하면 discounting 하기 전은 다음과 같다.
corpus 양이 한정되어 있으므로


Bigram의경우)
집합 A와 B를 정의
𝐴{𝑤|𝑐(𝑤_(𝑖−1)*𝑤)>0} 관측됨 A,
B{𝑤|𝑐(𝑤_(𝑖−1)*𝑤) = 0} 관측 안됨 B
이 때 Back-off 모델에서 Unseen N-gram의 확률을 다음과 같이 정의
alpha 에 의해서 모든 조건부 확률의 합이 1이 되게 만들어버리는 alpha를 찾음


예)


11단어 중,
<s>을 제외한 다른 단어들의 개수는 8단어로 구성되어 있음
Ache (1번) => log(1/8)
Cay (2번) => log(2/8)

<s>는 의미가 없기 때문에 가장 작은 값을 주고 싶기 때문에 제일 작은 log probabilaty = -99
back-off 수정 알고리즘


1. n_r 구하기
- bigram language 모델 만들기
- n1(한 번 나온 tuple) = 4
- n2(두 번 나온 tuple) = 2
2. Good-Turing estimate이가능한Max count 값을찾는다
- maximum r(good turing estimate가 가능한 max count) = 1 (n_r, n_(r+1)모두 있음)
3.
2에서구한값을토대로 𝑑_𝑟값을구한다.
A = {Cay, K.}
B = {</s>, Ache, <s>}->count가 없는 집합
두 개의 여집합 관계
A집합(seen들의 합)의 조건부 확률을 더하면 1
분모를 강제로 1씩 늘렸음

나머지 1/4는 unseen에 보내줌
1/4가 나오게 alpha를 고정시켜줌
α(</s>)*(Pr(</s>)/Pr(Adr)) = 1/4
Pr(</s>)=3/8
Pr(Adr)=1/8
인간 SRIM이 돼서 만들수 있으면 완벽 이해한 거! 인간 SRIM 하자
9.1.3 Language model scale factor

ㅇ 음향 모델의 생성확률 𝑷(𝑶|𝑾)는 매 frame마다 𝒂_𝒊𝒋 *𝒃_𝒋(𝒐_𝒕)가 곱해진다. 반면, 𝑷(𝑾)는 매 단어마다 𝑃(𝑤_𝑖|𝑤_(𝑖−2),𝑤_(𝑖−1)가 곱해진다.
ㅇ 따라서 음향 모델의 생성확률의 영향이 상대적으로 훨씬 크다.
ㅇ 이 문제점을 보완하기 위해, 언어 모델 Scaling factor alpha를 이용하여 𝑷(𝑶|𝑾)𝑷(𝑾)를 아래와 같이 계산한다.
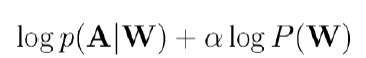
α 는 실험을 통해 계산된다. 영어뉴스 인식의 경우α 는 보통 2.0정도가 사용된다.
9.1.4 Text corpora nomalization
ㅇ 코퍼스는 사용하기 전에 정규화 되어야 함
- 사용할 수 없는 부분들은 (예: 표와 같은)폐기 되어야하고, 데이터는 표준형식으로 저장해야 함.
- 문장들은 개별적으로 태그를 지정하며, 숫자/ 날짜는 발음에 따라 처리 해야 함
언어 모델 평가 척도(Perplexity) 중요!
ㅇ연속 음성인식용 언어 모델의 품질은 음성인식율로 평가하는 것이 가장 좋다. -> perplexity 사용

평가 척도가 음수로 나오면 좋지 않음 -> 직관성을 부여하기 위해 - 붙여줌
n-> 무한대, 우리가 모은 corpus가 계속 커짐
ㅇ n-gram 생성 확률의 기하평균
- 어휘의 크기가 10만인 경우 최악의 언어모델은 어떤 언어모델인가?
- 비슷한 예로,내일 일기예보를 하는데 최악의 일기예보는 무엇인가?
맑을 확률1/3, 흐릴 확률1/3, 비올 확률1/3
일기예보가 절대 틀리지 않지만, 아무런 정보를 주지 않음
N개의 카테고리가 가지는 확률이 각각 1/n인 경우 엔트로피가 가장 높음
ㅇ 따라서 어휘의 크기가 10만의 경우 최악의 언어모델은 현재 단어로써 어휘 내의 첫 번째 단어에 대해 생성확률 1/10만, 어휘 내의 두 번째 단어에 대해서 1/10만, …, 어휘 내의 10만 번째 단어에 대해서 1/10만의 확률을 생성하는 언어 모델임
ㅇ 앞 페이지의 최악의 언어모델의 경우, 평균 단어별 n-gram생성 확률의 기하평균은 1/10만이고 PP=10만이 됨(기하평균의 역수)
ㅇ 따라서 PP는 언어모델에 의해 추정되는 다음 단어의 평균 수(average branching factor)로 이해 할 수 있음
ㅇ 동일한 어휘 크기와도 메인에 대해서, PP가 작은 언어모델이 일반적으로 좋은 언어 모델임
- PP의 이론상 최대값은? :어휘의 크기
- PP의 이론상 최소값은? : 1
음성을 듣지 않고 지금까지 나온 단어만을 가지고 다음 단어가 정확히 예측된다는 의미임. 그러나 이는 불가능 함
인반적으로 perplexity가 감소하면 word error rate 도 감소함
'대학원 수업 > 음성인식' 카테고리의 다른 글
| [Chapter7] self-attention (0) | 2023.06.17 |
|---|---|
| [Chapter9]언어모델(4)-DNN 기반 언어모델 (0) | 2023.05.31 |
| [Chapter9]언어모델(1) - ~smoothing (0) | 2023.05.17 |
| 중간고사 (0) | 2023.04.19 |
| [음성인식2] - 입/출력 end 복잡도 분석 (0) | 2023.03.15 |



