클러스터링

패턴인식 문제로 공식화 가능

 

고객 - 샘플 / 샘플을 특징(직업, 월평균 구매액) 벡터로 표현

유사한 (거리가 가까운 )샘플 집합을 군집이라 함

 

군집화 표현을 위해서는

1)거리 척도, 2)유사한 샘플을 군집으로 만드는 알고리즘

필요

 

지도 학습과 비지도 학습

지도 학습 :  각 샘플이 그가 속한 부류를 안다

비지도 : 샘플 부류 정보 없음

군집화는 비지도 학습 / 군집이 몇 개인지도 잘 모름

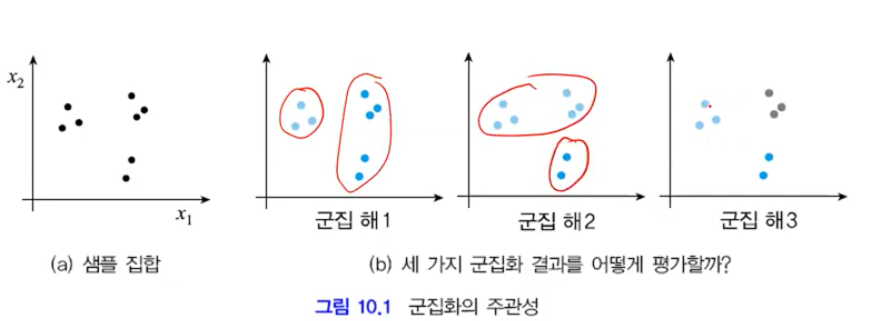
서로 유사해 보이는 샘플들 끼리 군집화

거리와 유사도는 반대 개념으로 하나를 알면 공식을 이용하여 다른 것을 쉽게 계산할 수 있음

 

 

특징 값의 종류

양적 특징(수량) 거리 개념 없음 / 나이, 연봉, 월평균 구매액

질적 특징(순서값 : 반품 성향, 선호 물품 수준, 명칭값 : 직업, 성별) 거리 개념 없음

 

거리와 유사도 측정

distance metric

 

 

군집과 점 사이 거리

점-집합간의 거리 측정

평균을 대표로 삼은 / 다른 것들과 가장 가까운 샘플을 대표로 삼음

계산할 수 있겠죠??(??)

 

군집과 군집 사이 거리도 구해줌 

온라인 필기 인식의 경우 Levenshtein edit distance 교정 거리 활용

 

다양한 군집 알고리즘

다양한 군집 모양에 따라 다른 군집 알고리즘을 사용해줘야함

군집화 알고리즘 분류 체계

계층 군집화 : 응집 (bottom up) 덴드로그램 / 분열(top down)

(bottom up)duration이 길면 안정화 그룹임 / K에서 잘라준다

 

(top-down)전체를 하나로 보고 군집간의 평균거리가 커지는 방향으로 분할해나감

순차 알고리즘

k-means 알고리즘 내리막 경사범, 빠르고, 전역 최적점 보장 못함 , 외톨이에 민감(k-medoids는 덜 민감)

평균값을 예측하고 평균값들에 의해 샘플들 분할 /분할 된 샘플 업데이트 / 업데이트된 평균에 의해 sample 분할 / 더 이상 분할되는 업데이트가 없을때까지 분할

모델 기반 알고리즘 - 가우시언 모델 기반 EM 알고리즘

 

신경망 - 자기 조직화맵

분할 군집화 :

신경망, 통계적 탐색