공부 정리 블로그
정리!!! 본문
1. SVM 개념
각각의 class에 있는 sample들과 만나게 되는 가장 처음 sample(support vector) 중에 여백(margin)을 가장 크게 하는 w를 찾는 문제
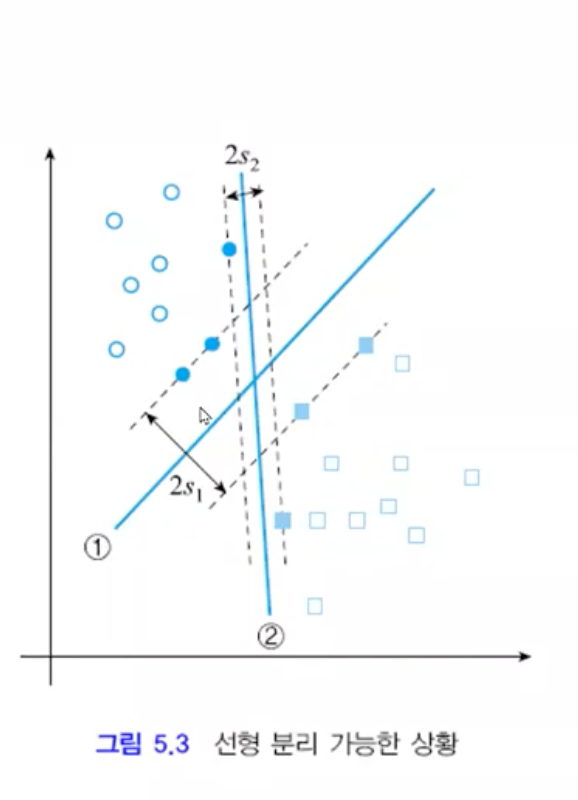



2차함수 문제가 되어 아래로 볼록이므로 해가 유일하고 구한 해는 전역 최적점을 보장한다.
문제의 난이도가 N개의 선형 부등식을 조건으로 가진 2차 함수 최적화 문제가 됨
조건부 최적화 문제는 라그랑제 승수로 접근(lagrange multiplier)

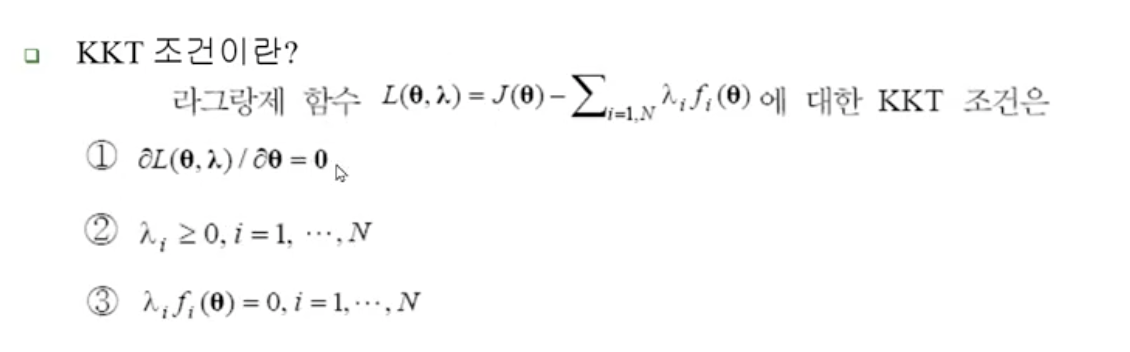
라그랑제 승수 방법을 통해 목적 함수와 조건을 하나의 식으로 만들고 KKT 조건을 이용하여 라그랑제 함수를 최적화 하는 해를 구함
2차 함수 최적화 문제는 Wolfe 듀얼로 최댓값을 구하는 문제로 변환할 수 있어 조건이 등식 조건으로 되어 풀기 유리해진다.
이때 w와 b가 사라져 라그랑제 a를 찾는 문제로 변하며, 특징 벡터 x가 내적 형태로 나타 비선형으로 확장 발판이 마련된다.
*SVM 정리
SVM은 여백을 최대로하여 일반화 능력을 극대화시킴
SVM 목적과 매개 변수의 관계를 설정하고 여백을 공식화하여 목적함수로 삼는다(최대화 문제)
목적함수의 역수를 취하고 2차함수로 바꾸어 최소화 문제로 변형한다.
라그랑제 승수를 도입하고 문제의 볼록 성질을 이용하여 Wolfe 듀얼 문제로 변형한다.
라그랑제 함수를 최대화하는 문제가 되며 부등식이 등식 조건으로 바뀐다.
라그랑제 함수를 정리하여 w와 b가 없어지고 a만 남는다. 특징 벡터가 내적 형태로 나타나 비선형 SVM으로 확장하는 토대가 마련된다.
선형 분리 불가능한 경우 Cost function 도입 0=<a=< C
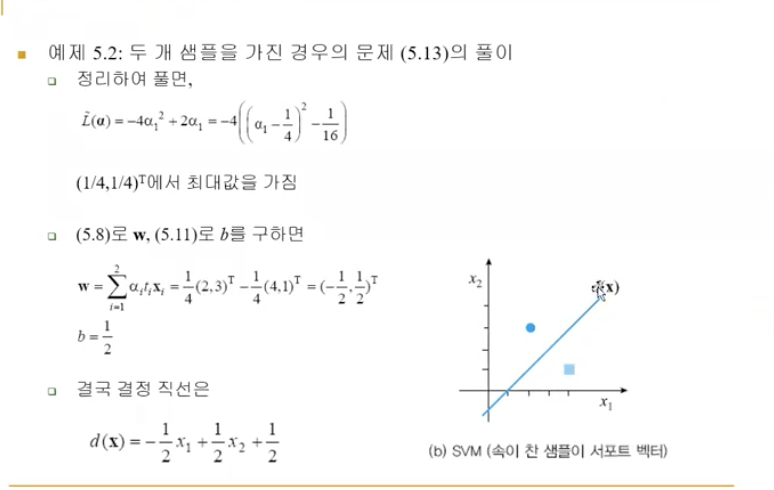
decision boundary 유도하는 공식, 실제 decision boundary 계산도 했지만 그런걸 물어보기는 좀..
아주 간단한 형태에 대해서 누가봐도 명확한 답이 보이는 경우에 간단한 예를 가지고 계산하는 건 의미가 있을 거 같은데
주어진 시간에 여러가지 계산을 하기는 좀 어려울 거 같음
2. 중요한 개념 SVM 은 선형 분리기인에 어떻게 선형 분리기를 이용해서 비선형 문제를 풀 수 있는가
커널 트릭을 이용하여 실제 계산은 L에서 이루어지지만 분류는 선형 분류에 유리한 H에서 수행
고차원으로 가서 선형적으로 풀 수 없는 문제를 풀게 함 하지만 noise가 발생하지는 않음
분류기의 성능을 높인 결과 (다항식 커널, RBF 커널, 하이퍼볼릭 텐젠트 커널)
3. hard / softmargin
Cost가 작으면 soft margin으로 오분류를 허용하는 범위가 넓어진다. 반대로 Cost가 클수록 오분류 허용이 줄어드는 hard magin이 된다. 일반적인 성능이 중요하므로 over fiting 된 hard margin 보다 soft margin의 성능이 더 좋다.
train 시점에 좋은 성능을 내는 것보다, test 시 좋은 성능을 내는 것이 더욱 중요하므로 test 시점에 오류가 적어지는 soft magin이 더 좋은 분류기라고 할 수 있다.
slack 변수
선형 분리 불가능한 경우, 0=<a 조건이 0=<a=<C로 변경되며, 슬랙 변수를 도입한다.
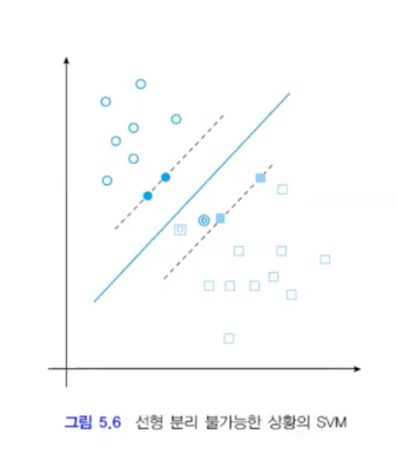

최소화 문제이기 때문에 C가 커지면 slack 변수항이 작아져야 하고, C가 작아지면 slack 변수항이 커져야한다.
C가 크면 hard margin으로 error허용 범위가 줄어들게 되고, C가 작아지면 오분류를 허용하는 범위가 넓은 softmargin이 된다.
=>여백을 될 수 있는 한 크게 하며, 동시에 0<(slack) 샘플의 수를 될 수 있는 한 적게하는 결정 초평면 방향 w를 찾는 문제
4. 그 과정에서 cost factor가 나옴
5. phi , mapping function
커널 평선에 대한 개념 설명 문제 : 어떤 수식이 벡터 내적을 포함할 때, 그 내적을 커널 함수로 대치하여 계산하는 기법
실제 계산은 L공간에서 K()의 계싼으로 이루어지므로, 고차원 공간 H에서 작업하는 효과를 가진다.
적용 예 Fisher LD의 커널 LD로의 확장, PCA를 커널 PCA(Principal component Analysis 차원축소 H->L) 로 확장
Linear discriminant
/ 간단한 계산 나오는 것도 가능
6. 커널 트릭을 이용해서 어떻게 비선형 문제를 linear로 푸는지를 이해
커널적용이 가능한 이유는 '특징 벡터가 내적 형태로만'나타나기 때문으로
커널 함수로 저차원에 선형 분리가 불가능한 문제를 고차원으로 매핑하여 선형 분리가 가능하게 만든다.
결과적으로 high space에서
7. 비선형이지만 고차원에서는 여전히 선형적인 문제
8. binary가 아닌 m개에서 어떻게 작동을 하고 학습을 하는지도 볼 것
x를 wk 로 분류하라. 이때, k = argmaxd_j(x)
즉, 특정 class로 분류될 확률이 제일 높은 쪽으로 분류한다.
9. decision tree 어떻게 노드를 선택하고 분할을 해야하는지 impurity가 감소하는 방향으로 분기
노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 분기한다. 자식 노드에는 가능한 같은 부류의 샘플들이 담겨야 하며, 이 동질성을 측정해 주는 기준이 불순도이다. 일반적으로 엔트로피로 측정하며 이외에도 지니 불순도, 오분류 불순도가 있다. 불손도 감소량을 정의하고 이것을기준 함수로 사용하여 불순도가 감소하는 방향으로 분기시킨다.
다른 방법으로는 투잉 기준이라느 것도 있음

node의 질문을 선택할때도 impurity 감소가 최대가되는 방향으로 question 선택
불순도 측정 방법은?
결정트리는 비계량, 계랑 모두 다를 수 있고 해석 가능함. 또한 속도가 빠르다
10. 스트링 levenshetein 알고리즘 이해해 오기
교정 거리는 삽입, 삭제, 대치 등의 연산 비용에 따라 거리를 측정하는 방식으로 Levenshetein은 그 중 하나이다. levenshetein은 삽입, 삭제, 대치 세 가지 연산을 사용하며, 거리 최적화 문제이다. edit distance가 작은 방향으로 움직이며, 최소 비용의 변환을 찾고 동적 프로그래밍 기법을 적용한다.
levenshetein은 초기화, 전방 계산, 역 주척 세 단계를 거친다. 그 외에도 교정 연산마다 비용을 다르게 할 수 있고 대치만 사용하면 해밍 거리가 되고, 삽임과 삭제만 사용하면 최장 공통 부분 스트링의 문제가 됨
텍스트 처리할 때 NLP에서 많이 사용하는 metric
11. 순차 데이터 Markov, HMM 차이가 무었인지
마코프 - state별로 하나씩 상태가 있음
HMM - 각각 state에서 어떤 관측값이 있을지 확률값으로 나타남
하나의 관측값에서 여러가지 상태값이 확률로 나타남
어떤 상태의 행렬이 나타남에 따라 관측값이 다르게 나타남
모든 가능한 상태값 들 중 가장 큰 확률을 가지는 상태의 관측값을 선택
12. 은닉 마코프에 대해 3가지 (평가, 디코딩, 학습)
평가 : 모델 theta가 주어진 상황에서, 관측벡터 O를 얻었을때, P(O|theta)? / 동적 프로그래밍 / 그녀가 일주일 연속으로 쇼핑만 할 확률은?

디코딩 : 모델이 주어진 상황에서 관측벡터 O를 얻었을 때, 최적 상태열은? (가장 가능성이 높은 날씨) / 동적 프로그래밍(Viterbi 알고리즘) /산책-산책-청소를 했다면 3일간 그곳 날씨는?

학습 : 훈련집합 X={O1,,,,On}이 주어졌을때, HMM의 매개 변수 theta는? / EM 알고리즘(Baum-Welch 알고리즘)
평가 디코딩은 간단한 예가 주어졌을 때 계산을 할 수 있으면 좋음

학습은 수식이 복잡해서 자세히 안 봄
8~9 장 특징 추출
13. 특징을 어떻게 선택을 해야하는가에 대한 일반적인 얘기
14. PCA, LDA
PCA 원래 정보 손실을 가장 적게 하면서 샘플의 차원을 낮춤. 샘플들이 퍼져있는 정도를 변환된 공간에서 얼마나 잘 유지하느냐를 척도로 삼으며, 이 척도는 분산으로 측정한다. 즉, 샘플들의 분산이 최대가 되는 축을 찾는 과정
LDA 분별력을 최대화하는 축으로 샘플을 투영. 부류간 퍼짐이 크고 부류내 퍼짐이 작은 것을 기본아이디어로 목적함수를 최대화 시킴
15. Fisher LD
차이가 뭐인지 / 계산을 직접 하라고 요구는 하지 않음!(컴라이브러리 이용해서 풀기 때문)
아이겐 벡터, 아이겐 벨류 d 4~5는 풀 수 있지만 그 이상은 손으로 못 품
16. 손으로 푸는 건 안하지만 sample을 주고 PCA를 풀었을 때, 아이겐 벨류가 어떻게 나올 것인지 그려봐
17. PCA / LDA 가 어떻게 다르게 나타나는지
18. 특징 선택을 하는 방법들이 어떤 것이 있고
추출된 특징 벡터 중에서 쓸모없거나 중복성이 강한 특징을 찾아 제거 한 후 차원을 낮추어 계산 속도를 향상 시키고 일반화 능력을 증대한다. 부류내 분산은 작고 부류간 분산은 큰 특징벡터 분포가 분별력이 가장 좋다.
19. 분별력의 관점에서 특징을 선택하는 몇가지 알고리즘을 봄
1. 임의 탐색 알고리즘 : 아무 생각없이 여기 저기 뒤져보는 순진한 알고리즘
2. 개별 특징 평가 알고리즘 : 부분 집합 선택 후 내림 차순으로 정리한 후 가장 좋은 트징 순으로 분류기 성능이 좋은 부분 집합을 선택
3. 전역 탐색 알고리즘 : 한정 분기로 접근(현재의 부분집합보다 하나의 작은 부분집합에서 가장 좋은 부분 집합을 찾음, 현재 부분집합보다 성능이 좋지 않을 시 버림, 탐색 공간은 적어지나 전역 조건을 만족한다는 가정하에 수행 d1이 성능이 좋지 않을 때 d2도 좋지 않음 / 하지만 일반적으로 이 조건을 만족하지 않음) / 더 좋은 해가 나오지 않을 거 같은 영역은 버림
4. 순차 탐색 알고리즘 : 특징 하나를 추가하는데, 가장 킁 성능 증가를 가죠오는 특징을 F2에서 F1으로 이동시킴 / 반대로 제거 시 가장 적은 성능 저하를 가져오는 특징을 F1에서 F2로 이동시킴 / 모든 순차 탐색 알고리즘은 욕심 greedy 알고리즘으로 전역 최적점이 아닌 지역 최적점에 빠질 가능성이 크다
분별력 측정
특징 벡터 x가 얼마나 좋은지의 척도를 분별력 / 부류 분리 능력이라 부르며
1. 다이버전스 - 확률 분포 간의 거리를 이용하여 분포들 간의 거리를 멀게해주는 특징 벡터 일수록 좋음 하지만 차원의 저주 문제를 그대로 간직함
2. 훈련 샘플의 거리 고려 - 훈련 집합에 있는 샘플을 가지고 직접 거리를 측정(현실 적용이 쉬움)
3. 분류기 성능 - SVM 분류기 수행 후 그 성능을 특징 벡터 x의 분별력으로 취함, 하지만 학습이 필요해 시간이 오래 걸리지만 정확도가 가장 높다.
세 가지를 척도로 삼을 수 있다.
20. 클러스터링의 대표적인
거리계산 방법을 어떻게 선택하느냐에 따라 군집화 방법이 바뀜
21. 덴드로그램 (중요) hireachical
22. k-means
K-means 알고리즘은 내리막 경사법으로 빠르지만 전역 최적점을 보장하지 못하고 outlier에 민감하다.(k-medoids로 덜 민감하게 만듦)
샘플들간의 평균값을 예측하고 예측된 평균값들에 의해 샘플들을 분할한다.
분활된 샘플들을 업데이트 하고 이렇게 업데이트 된 평균에 의해 sample을 다시 분할 한다. 더 이상 분할되는 sample들이 없을 때 까지 업데이트 함
'대학원 수업 > 패턴인식' 카테고리의 다른 글
| 클러스터링 (0) | 2022.12.20 |
|---|---|
| 특징 선택 (0) | 2022.12.19 |
| 특징 추출3 -Fisher의 선형 분별 (0) | 2022.12.19 |
| 특징추출2- 주성분 분석 (0) | 2022.12.19 |
| 특징 추출1- 퓨리에 변환 (0) | 2022.12.19 |




