[SOCIAL MEDIA MINING1] - graph 기초
Social Media
Social Media Mining Challenges
1. Big Data Paradox : 빅 데이터의 분석과 해석에 있어서 편향과 제한을 야기
Social media data is big, yet not evenly distributed.
Often little data is available for an individual
2. Obtaining Sufficient Samples : 과연 샘플 데이터가 모든 data를 대표할 수 있을 것인가
3. Noise Removal Fallacy : 전처리에 대한 어려움
4. Evaluation Dilemma : ground truth가 없을 때, 어떻게 분석의 정확도를 높일 수 있을까
Graph
• A network is a graph.
– Elements of the network have meanings
• Network problems can usually be represented in terms of graph theory
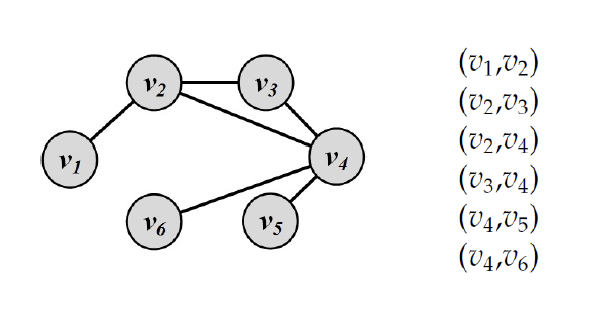
A network is a graph, or a collection of points connected by lines
• Points are referred to as nodes, actors, or vertices (plural of vertex)
• Connections are referred to as edges or ties

The size of the graph is |V| = n(node)
V = {v1, v2, ..., vn}
Number is edges (size of the edge-set) is denoted as |E| = m
E = {e1, e2, ..., en}
Graph 종류

Neighborhood and Degree (In-degree, out-degree)
neighbor : node에서 edge로 연결된 노드들의 집합 N(v)
- 방향 그래프에서는 들어오는 이웃을 N_in(v)라고 하며, 노드로부터 나가는 이웃을 N_out(v)라고 합니다.
degree : 한 노드에 연결된 edge의 개수를 그 노드의 degree라고 함(neighbor의 크기)
Degree and Degree Distribution
Theorem 1. degree의 총합은 edges 개수의 2배와 같다

Lemma1. degree가 홀수인 node의 개수는 짝수임
Lemma2. directed graph에서 in-degree차수 합, out-degree차수 합은 같음

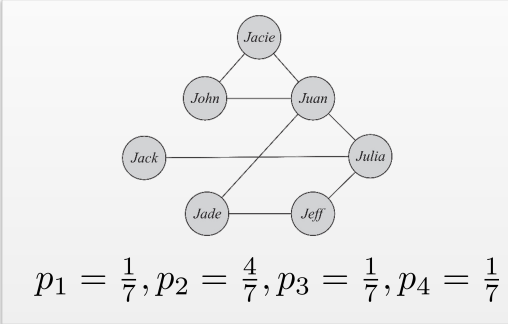
Degree Distribution
Graph Representation
We are seeking representations that can store these two sets in a way such that
– Does not lose information
– Can be manipulated easily by computers
– Can have mathematical methods applied easily
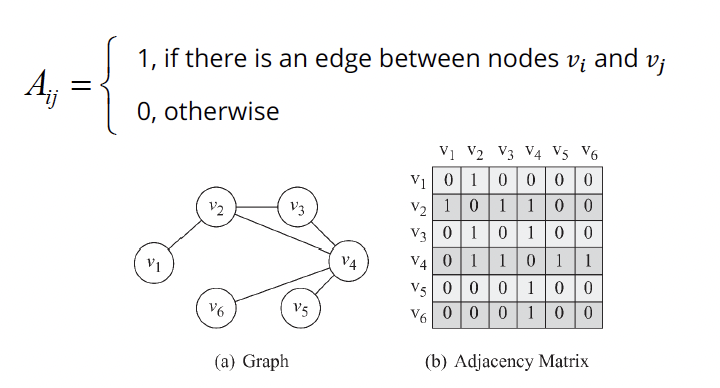
Adjacency Matrix (a.k.a. sociomatrix)
Adjacency List

Edge List