[음성신호처리2]푸리에 급수, 푸리에 변환, Discrete-Time Signals

Brief History of Automatic Speech Recognition (1)

•1960sNeural

- networks for phoneme recognition

인식을 위한 기본단위로 쪼개놓은 것 / 발음 종류로 구별해 놓은 것 phoneme

- Major breakthroughs

아날로그 신호인 음성을 continuous로 바꾼 것을 fourier transform라 한다

입력 신호를 디지털 신호로 바꿈

1. sampling

2. 각 sample 값들을 descret/ amplitude 관점으로 -> digital signal (숫자의 sequence 로 wave form 표현)

숫자의 vector array로 봄

- Three spectral analysis techniques

1. FFT (Fast Fourier transform)

연산을 빠르게 하기 위해 FFT 사용

2의 지수승의 sequece로 매우 빠르게 계산할 수 있음

 

2.LPC (linear predictive coding)

음성에서 메시지를 전달하는 부분 vocal track

특정 시점에서는 linear filter filter의 coeficient 를 알면 vocal track을 알 수 있음

filter의 coeficient를 찾는 것

입력 신호에 대해서 메세지 정보를 적절히 추론할 수 있고

초창기에 많이 사용했지만 얼마 지나지 않아서 안씀

왜?

noise에 취약

3. Cepstral(or homomorphic) analysis

메세지에 해당하는 정보를 low 로 보내서 메세지로 해당하는 것만 선택적으로 뽑기 위해(스피커는 버림)

 

- Pattern matching

1. DTW (dynamic time warping)

2. HMM (hidden Markov model)

 

•1970s

- ARPA speech-understanding project -CMU

 

•1980s

- Database: Large corpora

1. TIMIT: one of the most widely used hand-labeled phonetic corpora

2. RM: the grammar had a greater perplexity.

- Front ends: Mel cepstrum, PLP, delta cepstralcoefficients

wave form으로부터 음성의 feature를 뽑는 방식으로 많이 쓰는 테크닉

mel cepstrum

mel spectrum을 cepstrum으로 변환 시킨 것

달팽이관 원리 차용

mel scale로 쪼갬

 

PLP

노이즈에 robust 하게 해보자

귀가 처리를 하는 방식을 모사

 

delta cepstral coefficients

시간에 따라 사람의 음성은 음운의 sequence를 발음 

시간에 따라 다른 spectrum을 가진 것들이 순차적으로 발음됨

frame별 차이를 중점으로 입력으로 받아들임

시간의 차이를 세밀하게 받기 위해서

이웃한 frame의 차이를 구하고 그 차이에 집중

 

- Pattern matching: HMM (HMM ToolKit)

 

•Recent works

- Broadcast News transcription vs. Wall Street Journal transcription

- Conversational speech: Switchboard and Call Home

 

ASR이 어려운 이유

•Natural speech is continuous. Coarticulation/연속적임(연음)

•Variabilities from speaking rate, pronunciations, and contexts/(속도, 발음이 다양)

•Large vocabulary size/(신조어)

•Background noise, channel characteristics, microphone characteristics, and room acoustics/(배경소음, 환경 등 영향 고려)

1. phoneme의 sequence 이므로 continuous -> 연음 발생 coarticulation

2. 사람마다 발음, 속도 제각각

3. 큰 단어 사이즈

1~3은 딥러닝으로 어느정도 해결

4. 어느정도 마이크에 노이즈 있음, 스피커와 마이크 사이 거리가 가까우면 상관 없지만 ai 스피커/ 가전제품 음성인식으로 거리가 멀어지면 이 사이에 어쿠스틱 채널 생성(위치에 따라 다 달라짐) / 마이크의 특성에 따라 받아들이는 정보, 성분들이 달라짐 / 방의 반향이 심하냐, 얼마 없냐, 노이즈가 얼마나 있느냐 를 고려해야함

 

ASR Dimensions

ASR(Automatic Speech Recognition, 자동 음성 인식) 차원의 관점에서, 다양한 작업 매개 변수(Task parameters)가 있습니다. 이 매개 변수는 다음과 같은 요소들을 고려합니다:

1. 화자 종속 또는 화자 비종속(Speaker dependent or speaker independent): ASR 시스템이 개별 화자의 음성을 인식하는지, 여러 화자의 음성을 인식하는지에 대한 설정입니다.
2. 고립된 음성, 연속된 음성, 키워드(Keywords): ASR 시스템이 고립된 음성(한 문장씩 녹음된 음성), 연속된 음성(연속적인 대화) 또는 특정 키워드를 인식하는지에 대한 설정입니다.
3. 어휘 크기(Lexicon size): ASR 시스템이 처리할 수 있는 어휘의 크기를 의미합니다. 더 큰 어휘 크기는 더 다양한 단어와 문장을 처리할 수 있지만, 모델의 복잡성이 증가할 수 있습니다.
4. Perplexity: 문법 및 예측 제약 조건을 고려하여 다음 단어에 대한 불확실성의 양을 나타내는 지표입니다. 낮은 perplexity는 더 정확한 다음 단어 예측을 나타냅니다.
5. 말하는 스타일(Speaking style): 대화 형태의 음성 또는 낭독 형태의 음성과 같은 말하는 스타일에 대한 설정입니다.
6. 녹음 조건(Recording conditions): 음성 녹음 시의 대역폭, 노이즈 레벨 등과 같은 녹음 조건에 대한 설정입니다.
7. 샘플 도메인(Sample domains): ASR 시스템이 인식해야 하는 음성 샘플의 도메인에 대한 설정입니다. 예를 들어, B, C, D, E, G, P, T, V, Z와 같은 도메인이 포함될 수 있습니다.

"E set"은 Automatic Speech Recognition (ASR)에서 사용되는 음성 샘플의 도메인을 나타내는 용어로 사용될 수 있습니다. 이는 음성 인식 시스템이 훈련 및 테스트되는 음성 데이터의 일부로 사용되는 도메인의 약어입니다.

"E set"은 다양한 도메인을 나타내기 위해 사용되며, 각 도메인은 알파벳(E, B, C, D, G, P, T, V, Z 등)으로 표시됩니다. 예를 들어, E set은 말소리(Emotion)에 대한 도메인을 나타낼 수 있습니다. B set은 음성에 대한 배경 소음(Background noise) 도메인을 나타낼 수 있습니다. C set은 음성에 대한 채널(Carrier) 도메인을 나타낼 수 있습니다. D set은 음성에 대한 잡음(Distortion) 도메인을 나타낼 수 있습니다. 이러한 도메인은 ASR 시스템의 성능 평가와 테스트에서 중요한 역할을 합니다.

이러한 다양한 작업 매개 변수들은 ASR 시스템의 성능과 사용 가능한 기능을 결정하는데 중요한 역할을 합니다. 이러한 매개 변수들을 적절하게 설정하여 원하는 ASR 시스템의 동작을 조정할 수 있습니다.

Components of ASR

ASR (Automatic Speech Recognition)의 구성 요소를 설명해드리겠습니다:

1. Input acquisition (입력 획득): ASR 시스템의 첫 번째 단계는 입력 음성 데이터를 획득하는 과정입니다. 이 단계에서는 마이크, 녹음 장치, 또는 다른 음성 입력 소스를 통해 음성 데이터를 획득합니다.
2. Front end (전처리): 획득한 음성 데이터는 전처리 과정을 거쳐 ASR 시스템의 입력으로 사용됩니다. 이 과정에서는 음성 신호를 분석하고, 특성을 추출하고, 노이즈 제거, 음성 강조 등의 신호 처리 작업이 수행됩니다.
3. Local match (로컬 매치): 전처리된 음성 데이터는 ASR 시스템의 어쿠스틱 모델과 비교하여 가능한 음소 또는 음절 후보들을 생성하는 과정입니다. 이 단계에서는 입력 음성 데이터가 사전에 학습된 음소 또는 음절 모델과 어떻게 일치하는지를 결정합니다.
4. Global decoder (글로벌 디코더): 로컬 매치 단계에서 생성된 음소 또는 음절 후보들 중에서 가장 적합한 후보를 선택하기 위한 과정입니다. 이 단계에서는 문맥 정보를 고려하여 후보들을 비교하고, 가장 가능성이 높은 문장을 생성합니다.
5. Language model (언어 모델): ASR 시스템은 문장의 문법 및 언어적인 특성을 모델링하는 언어 모델을 사용합니다. 이 모델은 입력 음성 데이터와 로컬 매치, 글로벌 디코더의 결과를 통합하여 가장 적합한 문장을 선택하고 최종 출력을 생성합니다.

이러한 구성 요소들이 함께 작동하여 ASR 시스템은 음성 데이터를 획득하여 인식 가능한 텍스트로 변환하는 과정을 수행합니다. 각 구성 요소는 ASR 시스템의 성능과 정확성에 영향을 미치며, 각각의 과정은 다양한 알고리즘과 기술을 활용하여 구현될 수 있습니다.

 

Euler’s FORMULA

 

i = √-1

i =j 같은 것으로 봄

 

지수함수, 삼각함수(ㅠ), 복소수(i), 0,1같은 기본적인 수들을 결합

---

Fourier Series and Transform

 

Fourier Series(푸리에 급수)와 Fourier Transform(푸리에 변환)은 신호 처리와 통신 분야에서 주기 신호와 비주기 신호의 주파수 분석에 사용되는 수학적인 도구입니다.

https://angeloyeo.github.io/2019/06/23/Fourier_Series.html

푸리에 급수(Fourier Series) - 공돌이의 수학정리노트

 

수, 삼각함수(ㅠ), 복소수(i), 0,1같은 기본적인 수들을 결합

---

Fourier Series(푸리에 급수)와 Fourier Transform(푸리에 변환)은 신호 처리와 통신 분야에서 주기 신호와 비주기 신호의 주파수 분석에 사용되는 수학적인 도구입니다.

 

1. Fourier Series(푸리에 급수): Fourier Series는 주기 신호를 주파수 성분으로 분해하는 방법으로, 주기 신호를 다양한 주파수 성분으로 합성하는 과정을 나타냅니다. 푸리에 급수는 주기 신호를 주파수 성분들의 합으로 나타내는데, 각 주파수 성분은 복소 지수 함수로 표현됩니다. 이를 통해 주기 신호를 주파수 영역에서 분석할 수 있게 됩니다. 푸리에 급수는 연속적인 주기 신호에 대한 분석을 다루는 연속 푸리에 급수와, 이산적인 주기 신호에 대한 분석을 다루는 이산 푸리에 급수로 나뉘어지며, 주로 신호의 주파수 분석, 신호 압축, 신호 복원 등에 활용됩니다.
2. Fourier Transform(푸리에 변환): Fourier Transform은 비주기 신호를 주파수 성분으로 분석하는 방법으로, 비주기 신호를 무한개의 주파수 성분으로 분해하는 것을 의미합니다. 푸리에 변환은 시간 영역의 신호를 주파수 영역으로 변환하여 신호의 주파수 특성을 분석하고, 주파수 성분들의 강도와 위상을 알아내는데 사용됩니다. 푸리에 변환은 연속 시간 신호에 대한 연속 푸리에 변환과 이산 시간 신호에 대한 이산 푸리에 변환으로 나뉘어지며, 주로 신호 처리, 통신, 영상 처리, 음성 처리 등 다양한 분야에서 활용됩니다.

요약하면, Fourier Series는 주기 신호를 주파수 성분으로 분해하여 나타내는 것이고, Fourier Transform은 비주기 신호를 주파수 영역으로 변환하여 분석하는 것입니다. 두 가지 방법 모두 신호의 주파수 특성을 분석하고 이를 활용하는데 널리 사용되는 수학적인 도구입니다.

 

Fourier series(주기 신호) / Fourier transform(비주기 신호)

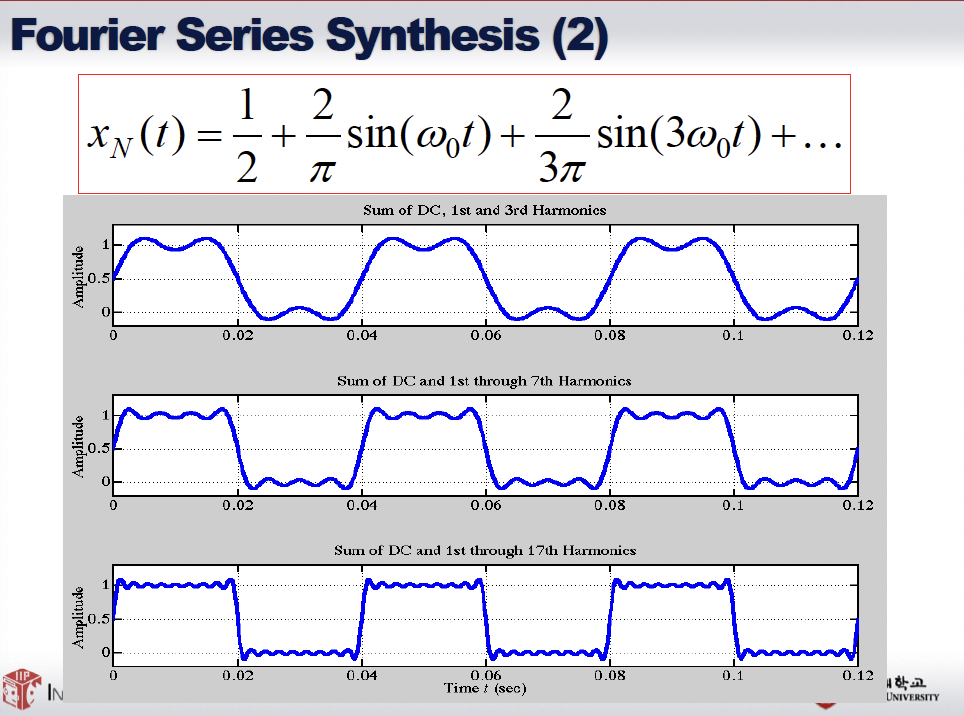
Fourier 분석과 합성은 시간 영역이 아닌 주파수 영역에서 신호를 분석하고 합성하는 수학적인 기술입니다.

Fourier Analysis - 분석

Fourier 분석은 신호를 주파수, 진폭, 위상이 다른 사인파 구성요소들로 분해하는 과정입니다. 이는 Fourier 변환 또는 이산 Fourier 변환 (DFT)을 사용하여 신호를 시간 영역에서 주파수 영역으로 변환하는 것으로 이루어집니다. Fourier 분석은 신호의 주파수 내용을 이해하게 해주며, 신호에 어떤 주파수가 존재하고 그들의 상대적인 강도를 식별하는 데 도움을 줍니다.

Fourier synthesis - 복원

Fourier 합성은 주파수 영역 표현을 기반으로 신호를 다시 재구성하는 과정입니다. 이는 역 Fourier 변환 또는 역 이산 Fourier 변환 (IDFT)을 사용하여 주파수 영역에서 얻은 사인파 구성요소들을 원래의 신호로 다시 결합하는 것으로 이루어집니다. Fourier 합성은 주파수, 진폭, 위상이 다른 사인파 구성요소들을 선택적으로 결합하여 새로운 신호를 생성하거나, 신호를 조작하거나, 필터링하는 데 사용될 수 있습니다.

 

[ Signal ] 푸리에 급수 (Fourier Series)

https://supermemi.tistory.com/95

[ Signal ] 푸리에 급수 (Fourier Series)

 

[ Signal ] 푸리에 변환 (Fourier Transform)-(1) 기본 유도과정

 

https://supermemi.tistory.com/entry/%ED%91%B8%EB%A6%AC%EC%97%90-%EB%B3%80%ED%99%98-Fourier-Transform-mathcalF-displaystyleu

[ Signal ] 푸리에 변환 (Fourier Transform) - (1) 기본 유도과정

[ Signal ] 푸리에 변환 (Fourier Transform)-(2) 다양한 함수의 푸리에 변환

https://supermemi.tistory.com/98

[ Signal ] 푸리에 변환 (Fourier Transform) - (2) 다양한 함수의 푸리에 변환

 

 

시간주기(T)가 무한대로 크면 반복을 보기 어렵기 때문에 비주기함수와 비슷하다고 여김

그렇게 때문에 주기 신호에서 시간주기 T를 무한으로 늘리면 비주기 신호로 볼 수 있으므로,

Fourier series를 비주기 함수에도 이용할 수 있게 됨 ->  푸리에 변환 !

 

Fourier series spectrum - discrete

Fourier transform spectrum - continuous

 

Discrete-Time Signals

https://angeloyeo.github.io/2022/01/14/sampling_CT_to_DT.html

연속 신호의 샘플링 - 공돌이의 수학정리노트

연속적인 신호를 smapling 해서 disceret한 신호로 변경

 

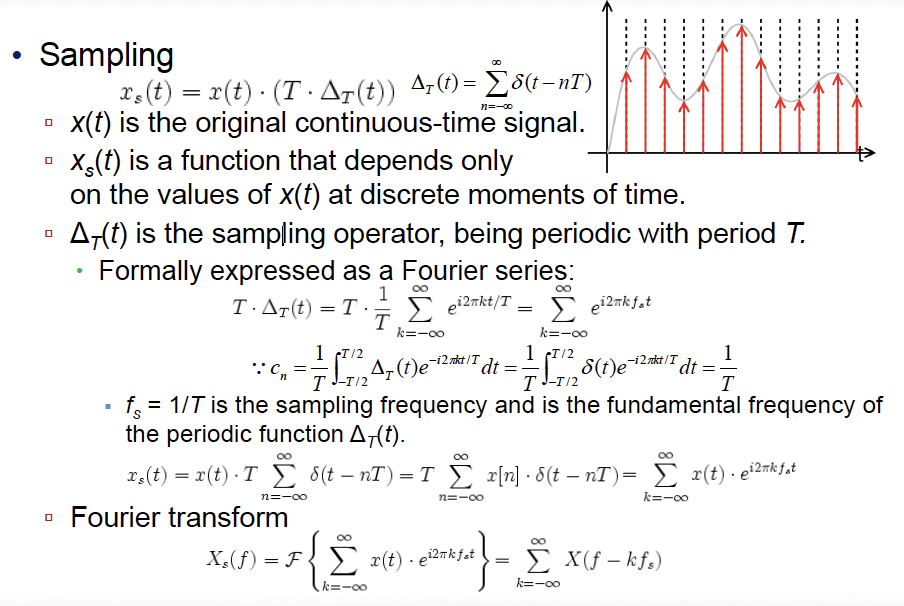
• x(t)는 원본의 연속시간 신호를 나타냅니다.(input)
• xs(t)는 x(t)의 값이 이산적인 순간의 시간에만 의존하는 함수입니다. 이를 통해 연속시간 신호를 이산시간 신호로 변환합니다.
• ΔT(t)는 T 주기를 가지는 샘플링 연산자(operator)로, xs(t)를 생성하는데 사용됩니다. ΔT(t)는 주어진 시간 간격 T마다 x(t)의 값을 추출합니다.
• 이를 푸리에 급수(Fourier series)로 표현하였습니다. 푸리에 급수는 주기적인 함수를 다양한 주파수 성분으로 분해하는 것을 의미합니다.

 

이산시간 신호의 샘플링은 원본 연속시간 신호를 특정 시간 간격으로 이산적인 순간에서만 값을 추출하여 이산시간 신호로 변환하는 과정입니다. 이를 푸리에 변환을 통해 주파수 성분을 분석하거나, 다양한 디지털 신호 처리 기법에 적용할 수 있습니다. 위의 내용은 샘플링과 관련된 이산시간 신호와 푸리에 변환의 개념들을 설명하고 있습니다.

 

Sampling Theorem(1)

1. 가장 높은 주파수가 정해져 있을 때, (Fmax = B)

2. Fs>=2Fmax(샘플링 비율)

1. 정보 손실 없이 샘플링하는 방법: 샘플링 과정에서 정보 손실을 최소화하기 위해서는 나이퀴스트(Nyquist) 샘플링 이론에 따라 충분한 샘플링 주파수로 샘플링을 수행해야 합니다. 나이퀴스트 샘플링 이론에 따르면, 신호의 최대 주파수의 2배 이상의 샘플링 주파수로 샘플링을 수행해야만 원본 신호를 완벽하게 복원할 수 있습니다. 이를 언더샘플링이나 오버샘플링 방법으로 구현할 수 있습니다. 언더샘플링은 샘플링 주파수를 낮추는 것으로 정보 손실이 발생할 수 있지만, 특정 조건을 충족할 때에만 가능하며, 신호의 주파수 스펙트럼이 일정 범위 내에 있을 때 유용합니다. 오버샘플링은 샘플링 주파수를 높이는 것으로 정보 손실은 없지만 불필요한 계산량이 증가하는 단점이 있습니다.

Fn = 2B = 2Fmax

(필요한 최소한의 )sampling rate == 신호 최대 주파수 2배 이상의 샘플링 주파수

interpolation (Sinc function)

 

 

원본 아날로그 신호를 샘플 값들을 기반으로 보간함수를 사용하여 정확하게 복원할 수 있음

보간 함수는 샘플 값들 사이의 값을 추정하는 함수로 사용

첫번째 그림에서 해당 아날로그 신호에 대해 sampling할 때, 최대주파수 B에 대해 2B만큼 해야 겹치지 않음

섞이면 복원이 불가능하기 때문에

마지막 그림은 sampling 된 것을 다시 아날로그로 복원하는 데, 이때 사용되는 것이 sinc Function

 

Discrete-Time Systems

이산시간신호 시스템 동작

https://angeloyeo.github.io/2022/01/11/LTI_system.html

선형 시불변(LTI) 시스템 - 공돌이의 수학정리노트

• input -> output (y[n] = T{x[n]})
• LTI system 조건 

1.

- Scaling ( 입출력 시스템이 있다)

- superposition principle: 

Homogeneity : T(aX1[n]) = aT(X1[n])

additivity : T(X1[n]+X2[n]) = T(X1[n])+T(X2[n])

 T(ax1[n]) + bx2[n]) = aT(x1[n]) +bT(x2[n]) /

위의 두 가지를 만족

principle of supereposition : 입력의 스칼라 배수에 대해 시스템 출력도 같은 비율로 변화, 입력의 합에 대해 시스탬의 출력도 합의 형태로 변화

 

2.

• time-invariant

"If y[n] = T{x[n]}), then y[n - n0] = T{x[n - n0]}"라는 부분은 시간 불변 시스템의 시간 불변성을 나타냅니다. 이는 입력 시그널에 대한 시간적인 이동이 시스템 출력에도 동일한 시간적인 이동을 일으킨다는 것을 의미합니다. 즉, 입력 시그널을 n0만큼 시간적으로 이동시켰을 때, 출력 시그널도 같은 n0만큼 시간적으로 이동한 것과 같다는 것을 의미합니다.

y[delay] = T(X[delay])

 

 

출력은 input X[n]과 impurse response인 h[x](LTI system/수학적 표현)의 convolution 으로 나타낼 수 있음

 

쓸만한지 판단하기 위한 척도들(BIBO, Causability)

system은 무한하게 커지면 의미가 없음

입력이 boundary 에 있을 때, 출력도 bound 안에 있음 -> BIBO(parctical)하게 활용 가능

BIBO

입력이 무한대로 커지더라도 출력이 무한대로 커지지 않음

시스템이 입력 신호의 크기를 제한하는 안정적인 동작을 가짐을 나타내는 지표

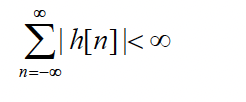
Causality(인과성)

시스템의 출력이 현재 시간 이후의 입력에 독립적

시스템이 미래의 입력에 대해 미리 반응하지 않음

=> 시스템의 출력이 현재 시간 이전의 입력에는 의존하지 않음

 

z-transform

https://under-bridge.tistory.com/6

Z transform