공부 정리 블로그
[SOCIAL MEDIA MINING4] - Network measure 본문
network measure
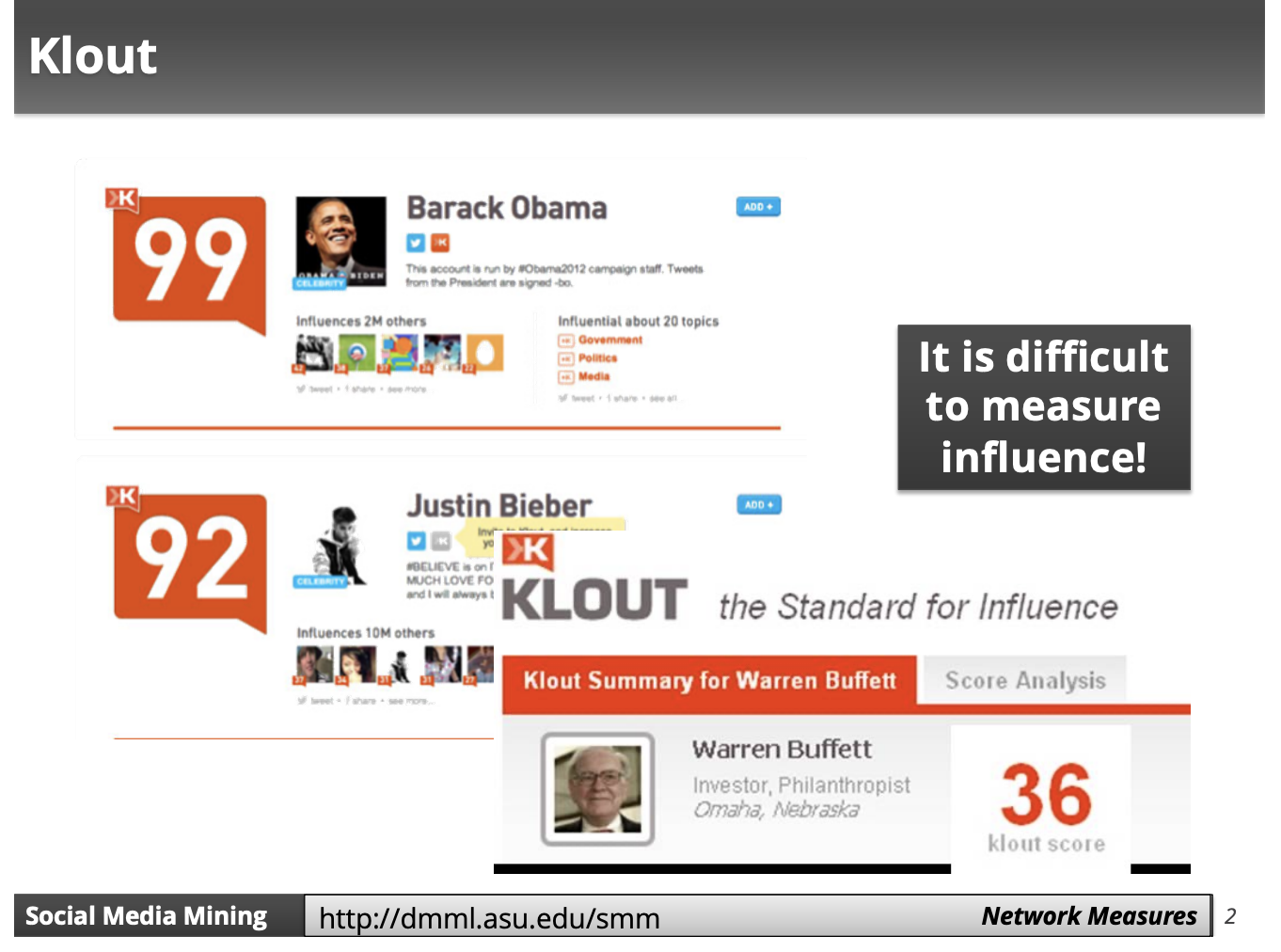
Why Do We Need Measures?
influence에 대한 measure(점수)
measure?
1. Centrality : 어떤 노드가 중심 노드인가?
2. interaction pattern(상호작용 pattern)
– Reciprocity and Transitivity
상호성(Reciprocity): 이는 친구들이 행동이나 행위에 대해 상호적으로 대응하는 경향을 말합니다.
전이성(Transitivity): 이는 친구들이 공통적인 친구나 유사한 사회적 연결을 가지는 경향을 말합니다.
– Balance and Status
균형(Balance): 이는 친구들이 균형 잡힌 관계를 유지하려는 경향을 말합니다. 즉, 시간, 관심, 지원 등의 자원을 대략적으로 균등하게 교환하는 관계를 유지하려는 경향
3. Smilality : 비슷한 생각을 가진 사람들이 누구인가?
= > 어떻게 하면 유사한 사람을 발견할 수 있을 것인가?
measure를 계량화 시켜서 사용자들간의 상호작용과 level 계량화 작업 필요
=> 이 사람이 얼마나 중요한 사람이고, interaction level이 얼마나 되는지는 measure를 알아야 사람들간의 유사도 측정이 가능해짐
Centrality
얼마나 중요한 사람인지 정량적으로 측정할지
정량화 시키는 간단한 방법
이 노드가 다른 노드와 얼마나 연결되어 있는지를 살펴봄
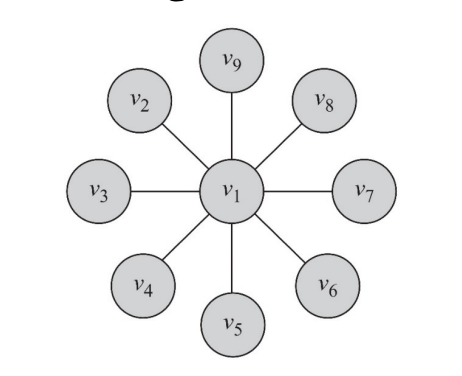
degree centrality가 높을수록 중요한 사람이다
direct한 노드의 개수를 파악
(length-n paths)는 n개까지 degree로 측정하겠다
방향성이 있는 sample의 경우
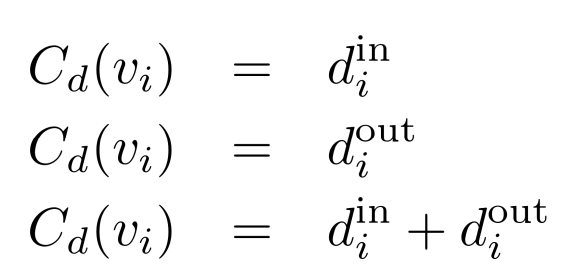
in-dgree 나를 팔로우 하는 사람들 (유명함)
out-dgree 내가 팔로우 하는 사람들 (성격 활발, 외향적)
팔로워가 많은 사람이 영향력이 높은 사람
팔로우가 많은 계정은 의미가 없는 숫자다
Normalized Degree Centrality
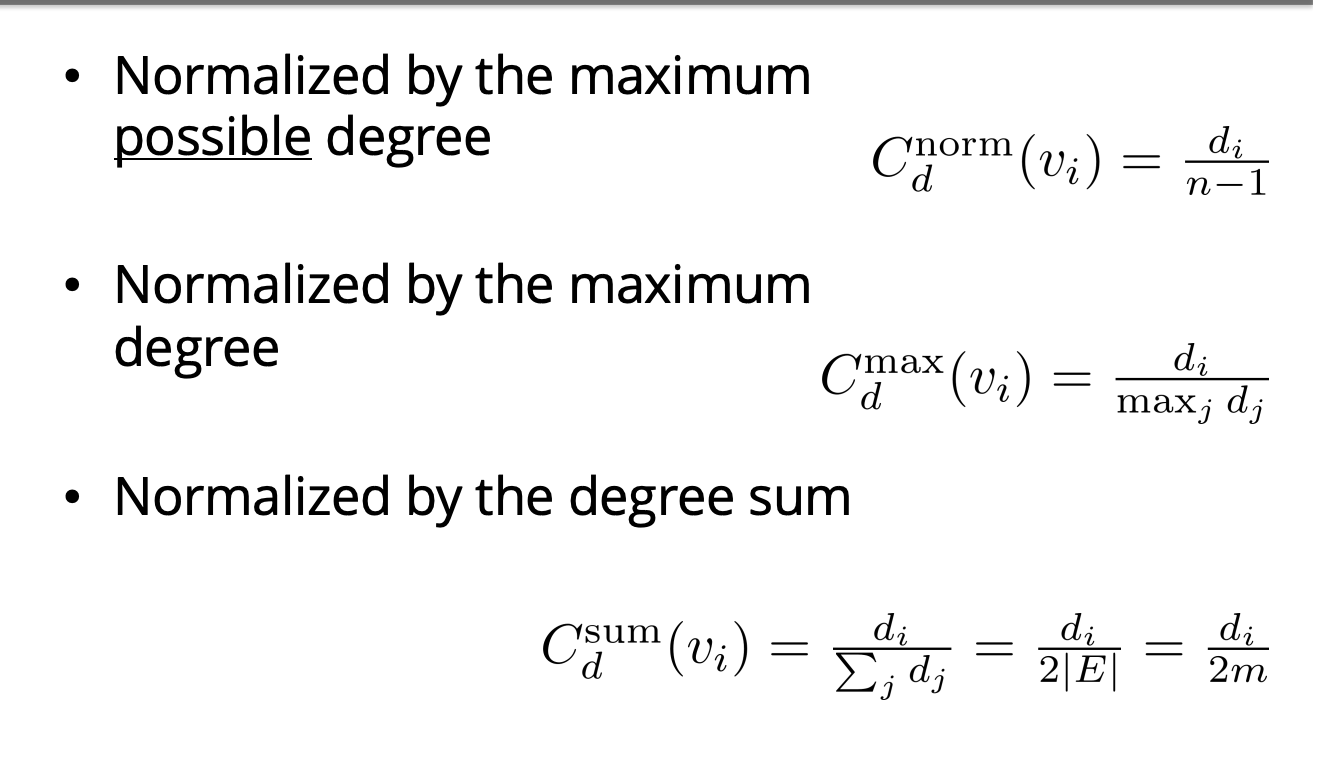
1에 가까울 수록 높음 / 0에 가까우면 낮음

Eigenvector Centrality
나를 팔로우하는 사람 중에서 유명인이 있으면 centrality가 높아짐
neighbor 중 중요한 사람을 고려하겠다
Formulation
칼럼 - incoming?

방향성이 있는 그래프에 적용했을 경우 문제가 생김
어떤 노드가 directed acyclic graph에서 centrality가 0 이 되는 것이 항상 있음
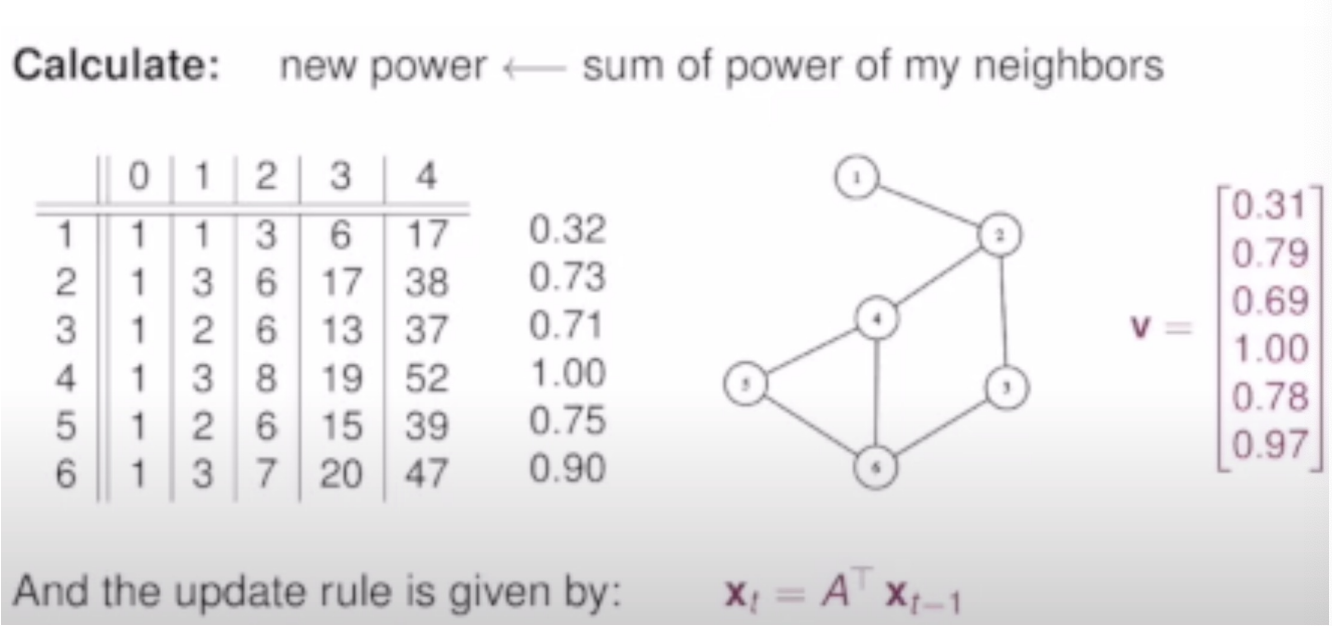
1. 처음에는 1로 초기화 시킴
2. neighbor에서 가져오겠음(2에서 인접한 1,4,3의 centrality를 가져옴)
ex) 2= (C1, C3, C4) C = centrality
3. 2번째 단계에서 구한 centrality를 고려해서 구하라
( 1~3 )반복 하면 가장 큰 eigen vector가 나옴
eigen vector 구하는 방법
수학적 / 반복 알고리즘(근사해서 구함)
Eigenvector Centrality 문제점
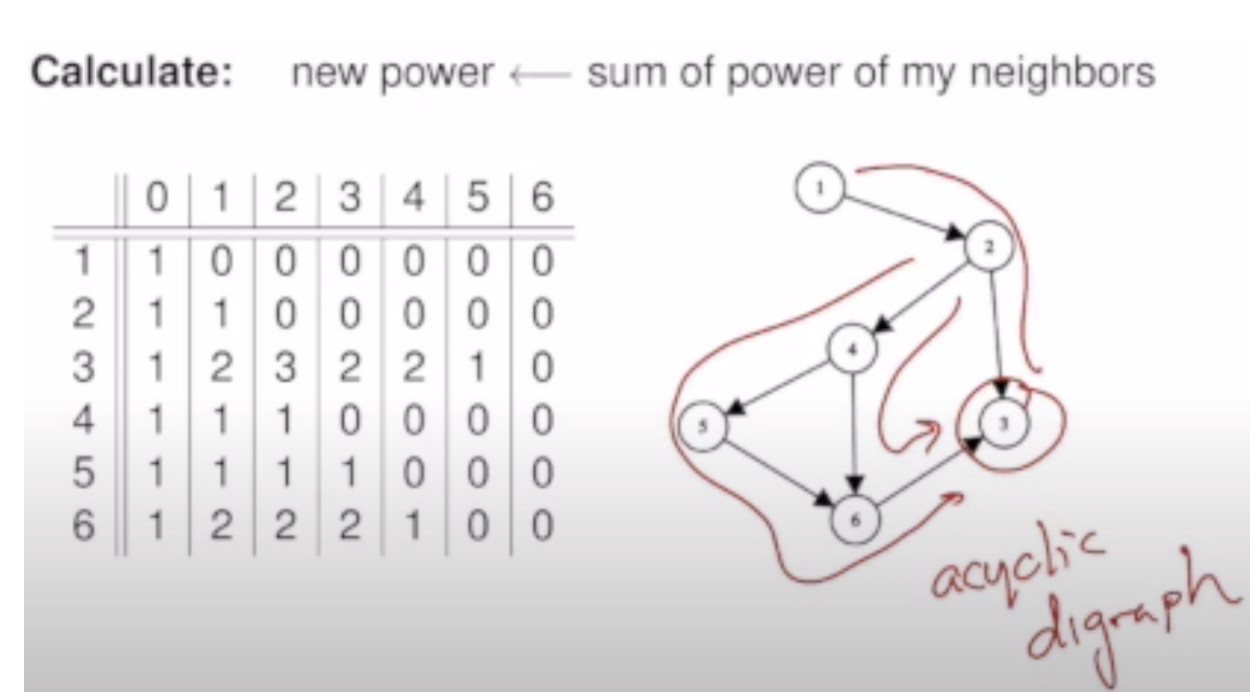
방향성이 있는 그래프의 경우 (비순환 그래프 / acyclic digraph)모두가 다 0이 되는 문제가 생김
순환이 안되는 문제 발생
문제 해결을 위해 bias를 추가한 Katz 사용
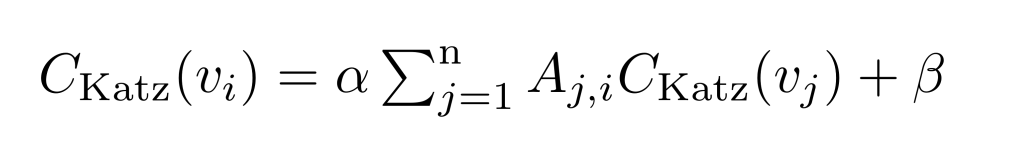
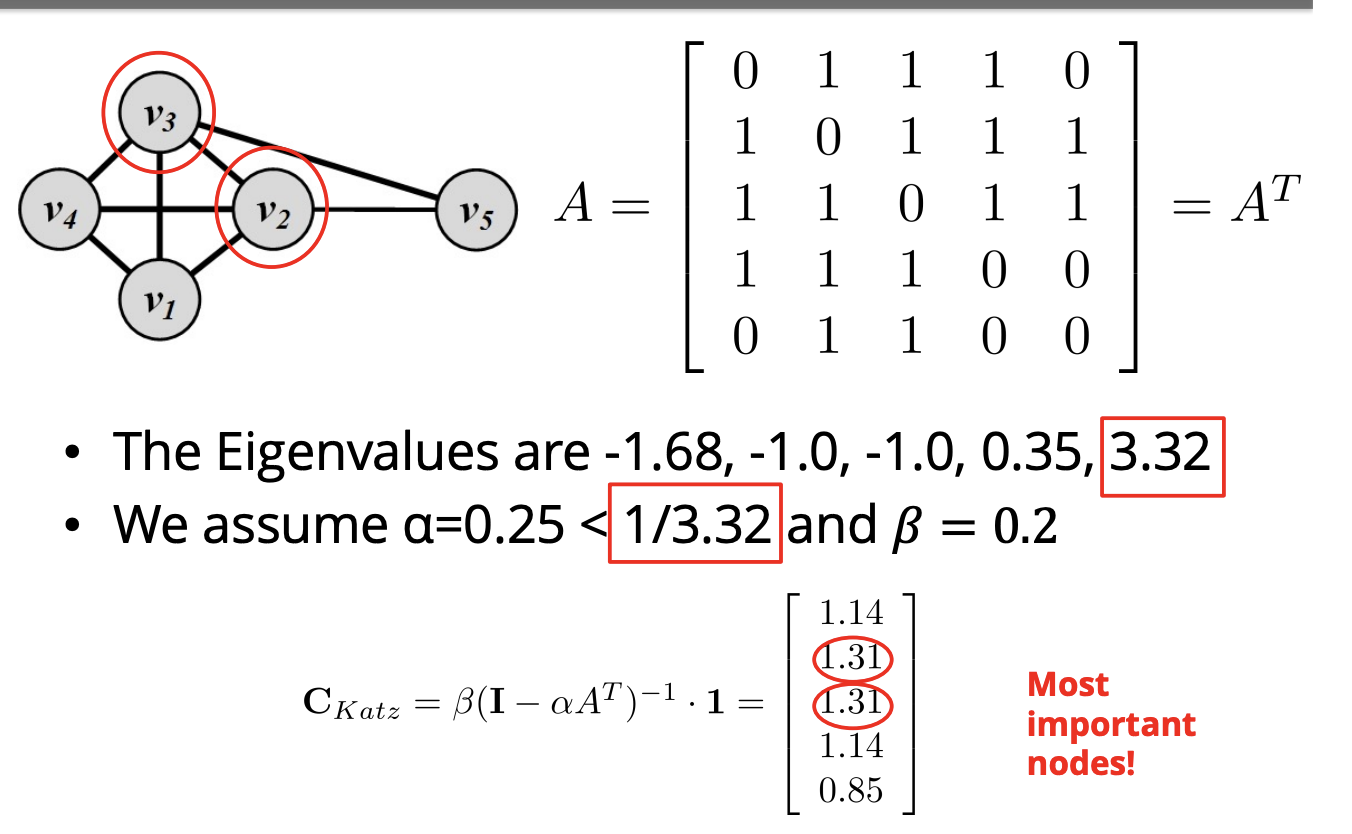
PageRank
Katz Centrality(카츠 중심성)는 네트워크에서 중요한 노드를 찾는 데에 사용되는 방법 중 하나입니다. 그러나 카츠 중심성은 방향성이 있는 그래프에서 한 가지 문제가 있습니다.
바로 한 노드가 권위있는 노드(높은 중심성)가 되면, 해당 노드는 그의 모든 아웃링크(나가는 연결)를 통해 중심성을 전달하는 것입니다. 이는 그 권위있는 노드를 알고 있는 모든 사람이 그의 권위를 알고 있는 것으로 간주되어, 실제로는 그의 권위를 알고 있는 사람들 중 일부만이 권위가 있는 것이 불합리한 결과를 초래할 수 있습니다.
이러한 문제를 해결하기 위한 방법으로는, 전달되는 중심성의 값을 해당 노드의 아웃링크 수(아웃디그리)로 나누는 것이 있습니다. 즉, 해당 노드의 아웃링크 수에 따라 전달되는 중심성의 값을 조절하여, 연결된 이웃 노드들이 원본 노드의 중심성의 일부만을 받게 됩니다.
이렇게 함으로써 원본 노드의 중심성이 모든 이웃 노드에 동등하게 전파되지 않고, 아웃링크 수에 따라 일정 비율로 전달되게 되어, 더 합리적인 결과를 얻을 수 있게 됩니다. 이 방법은 카츠 중심성의 문제를 해결하는 데에 사용되며, 그래프의 구조에 따라 적합한 값을 선택하여 사용할 수 있습니다.
page lank의 핵심 아이디어
가지고 올 때, out의 수를 고려해서 쪼개서 들고옴
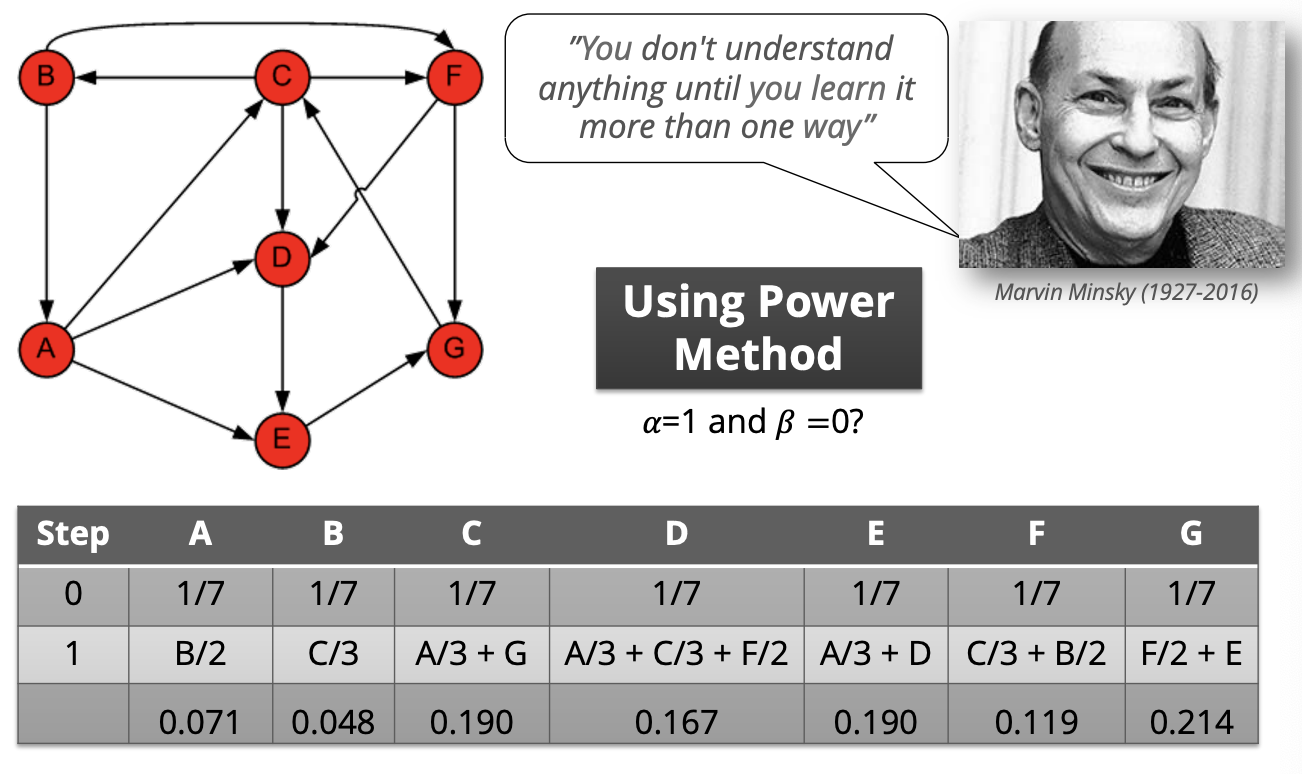
상대방의 centrality를 가져와서 내 것을 보완
1/ out dgree 만큼만 가져오겠다
Summary
Eigenvector Centrality(고유벡터 중심성)는 네트워크에서 중요한 노드를 찾는 데에 사용되는 방법 중 하나입니다. 이 방법은 노드의 중심성을 해당 노드의 인-이웃(in-neighbors)들의 중심성의 합으로 업데이트하는 방식을 사용합니다. 즉, 인-이웃들의 중심성을 모두 더한 값으로 해당 노드의 중심성을 갱신합니다.
Katz Centrality(카츠 중심성)는 각 노드가 일정 비율의 "자유로운(free)" 중요성을 가지는 방법입니다. 따라서 해당 노드의 중심성을 업데이트할 때, 인-이웃들의 중심성뿐만 아니라 일정 비율의 자유 중요성도 함께 고려됩니다.
PageRank(페이지랭크)는 중요성을 아웃-이웃(out-neighbors)들 사이에서 공평하게 분배하는 방법입니다. 즉, 해당 노드의 중심성을 아웃-이웃들 사이에서 동등하게 분배하여 업데이트합니다. 이 방법은 웹 페이지의 중요성을 평가하는 데에 사용되는데, 링크를 통해 다른 웹 페이지와 연결된 구조를 고려하여 중요성을 산정합니다.
Betweenness Centrality
Centrality in terms of how you connect others?
1. Beteweeness Centrality
얼마나 중요한 역할을 하고 있는지를 측정
s-> vi -> t /s->t 최단거리 = 1
vi 매우 중요
가능한 개수는
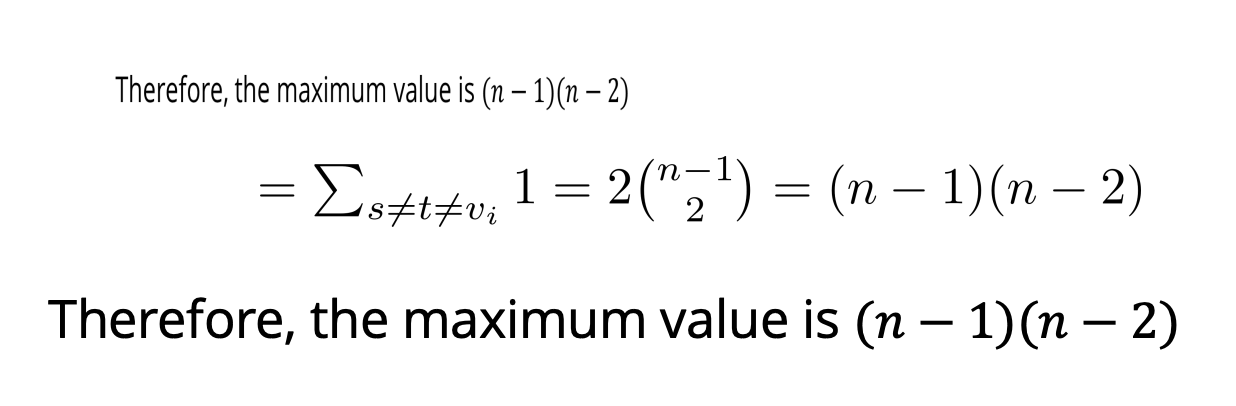
(s,t) (t,s) 두개가 나오므로 *2
노드의 개수 총 5개
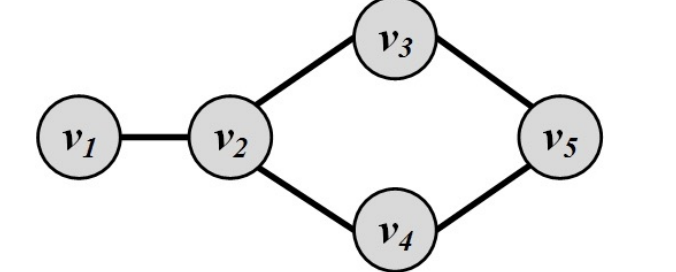
연결성 측면에서 중요한 노드 v2 (<-> v5)
v1 = 0

서로 다른 두 노드를 연결할 때 내가 얼마나 중요한 노드인지(bridge)
이 노드를 제거시키면 그래프가 쪼개짐
cf) 내가 얼마나 빨리 도달하게 하는지
closeness Centrality
influential/central node 허브역할
나를 통해서 다른 노드로 빠르게 도달
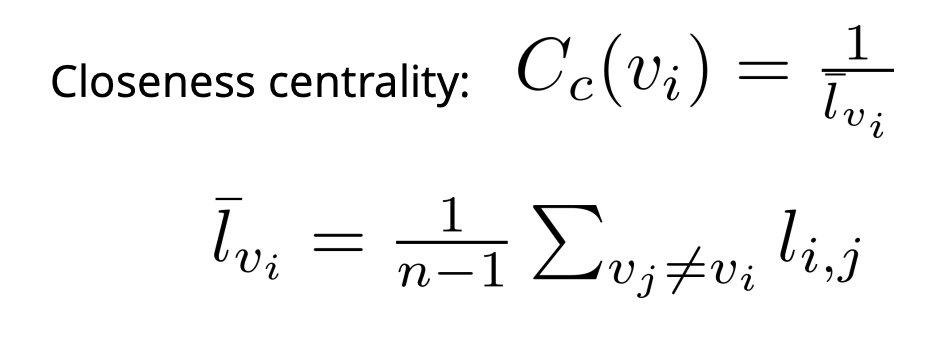
v1에서 다른 노드로 얼마나 빨리 도달하나
12 => v1->v2 최단 거리
Cv1 = 1 / ((12 + 13 + 14+ 15)/4)
v2를 통해 다른 노드로 빠르게 이동할 수 있음
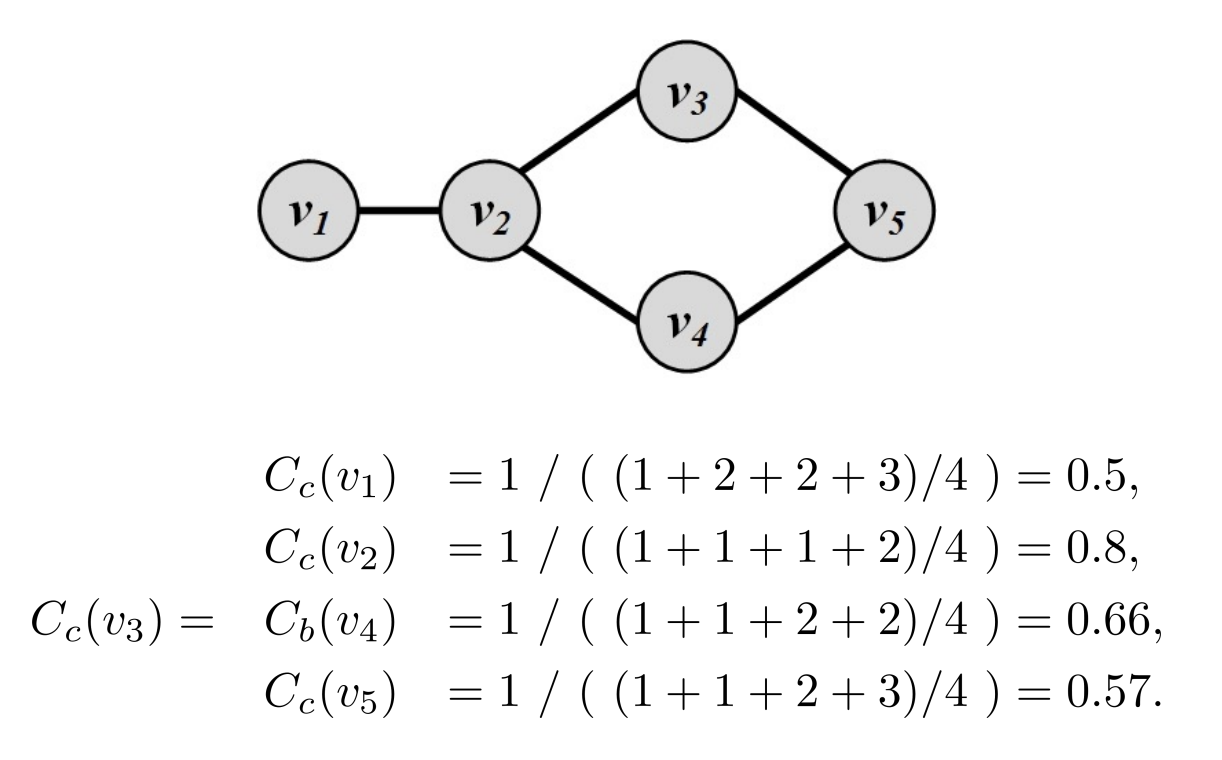
방향성 유무에 따라 centrality 달라짐
dgree centrality
(eigen / kartz / page lank 비교할 것)
'대학원 수업 > sns 분석' 카테고리의 다른 글
| [SOCIAL MEDIA MINING3] - Graph/NetworkTraversal Algorithms (0) | 2023.04.23 |
|---|---|
| [SOCIAL MEDIA MINING2] - types of graph (1) | 2023.04.23 |
| [SOCIAL MEDIA MINING1] - graph 기초 (0) | 2023.04.23 |
| [SOCIAL MEDIA MINING8] - Classification withNetwork Information (1) | 2023.04.18 |
| [SOCIAL MEDIA MINING5] - Centrality for agroup of nodes (0) | 2023.03.28 |




